In section 6.4 you will learn about three special types of parallelograms the Rhombus, Rectangle, and the Square. This section is very interesting and fun to study. There are breath taking corollaries and theorems in this section that will help you understand this section a whole lot easier.
The Rhombus:
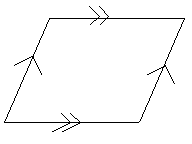
A Rhombus is a parallelogram with four congruent sides. A
Rhombus Corollary is a quadralateral only if it has four
congruent sides.
The Rectangle:
A Rectangle has four congruent sides. A Rectangle Corollary is
a quadralateral that is a rectangle only if it has four right angles.
The Square:
A Square is a shape with four right angles and four congruent
sides. A Square Corollary is a quadrilateral that is a square only
if it is a rhombus and a rectangle.
Notes/Tips:
* When solving problems that have to do with a rhombues set all sides equal to each other.
*Use properties of sides and angles of Rhombuses, Rectangles, and Squares.
*Theorems will help you solve the equations alot faster.
*Use Properties of Diagnols of Rhombuses, Rectangles and Squares.
Questions:
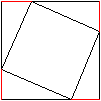
What information do you need to figure out that this is a Square?
Distance of AB=5x+10
Distance of BC=10x
Find the value of x. (Use the tips for help)Distance of AD=2y+3
Distance of DC=5y-6
O=65 degrees
Solve for y.(some information is less than they appear)
Consider rectangle JKLM shown in the figure.
If JL = 6y - 21 and MN = 2y + 9, find y.
Hint: The diagnols are congruent.
With all the information in the picture, can you tell if all sides of the square are congruent? Explain.
BEAST!!!
ReplyDelete